Overview

In recent years, a number of reinforcement learning (RL) methods have been proposed to explore complex environments which differ across episodes, such as procedurally-generated video games or embodied AI tasks. In this work, we show that the effectiveness of these methods critically relies on a count-based episodic term in their exploration bonus. As a result, despite their success in relatively simple, noise-free settings, these methods fall short in more realistic scenarios where the state space is vast and prone to noise. To address this limitation, we introduce Exploration via Elliptical Episodic Bonuses (E3B), a new method which extends count-based episodic bonuses to continuous state spaces and encourages an agent to explore states that are diverse under a learned embedding within each episode. The embedding is learned using an inverse dynamics model in order to capture controllable aspects of the environment. Our method sets a new state-of-the-art across 16 challenging tasks from the MiniHack suite, without requiring task-specific inductive biases. E3B also matches existing methods on sparse reward, pixel-based Vizdoom environments, and outperforms existing methods in reward-free exploration on Habitat, demonstrating that it can scale to high-dimensional pixel-based observations and realistic environments.

Introduction

Exploration in environments with sparse rewards is a fundamental challenge in reinforcement learning (RL). Exploration has been studied extensively both in theory and in the context of deep RL, and a number of empirically successful methods have been proposed, such as pseudocounts, intrinsic curiosity modules (ICM), and random network distillation (RND). These methods rely on intrinsically generated exploration bonuses that reward the agent for visiting states that are novel according to some measure, and have proven effective on hard exploration problems, as exemplified by the Atari games Montezuma’s Revenge and PitFall.

The approaches above are, however, designed for singleton RL tasks, where the agent is spawned in the same environment in every episode. Recently, several studies have found that RL agents exhibit poor generalization across environments, and that even minor changes to the environment can lead to substantial degradation in performance. This has motivated the creation of benchmarks in the Contextual Markov Decision Process (CMDP) framework, where different episodes correspond to different environments that nevertheless share certain characteristics. Examples of CMDPs include procedurally generated (PCG) environments or embodied AI tasks where the agent must generalize its behavior to unseen physical spaces at test time.

Figure 1: Examples of Contextual MDPs, where each episode corresponds to a different environment.

Recently, several methods have been proposed which have shown promising performance in PCG environments with sparse rewards, such as RIDE, AGAC and NovelD. These methods propose different intrinsic reward functions, such as the change in representation in a latent space, the divergence between the predictions of a policy and an adversary, or the difference between random network prediction errors at two consecutive states. Although not presented as a central algorithmic feature, these methods also include a count-based bonus which is computed at the episode level.

In this work, we take a closer look at exploration in CMDPs, where each episode corresponds to a different environment context. We first show that, surprisingly, the count-based episodic bonus that is often included as a heuristic is in fact essential for good performance, and current methods fail if it is omitted. Furthermore, due to this dependence on a count-based term, existing methods fail on more complex tasks with irrelevant features or dynamic entities, where each observation is rarely seen more than once. We find that performance can be improved by counting certain features extracted from the observations, rather than the observations themselves. However, different features are useful for different tasks, making it difficult to design a feature extractor that performs well across all tasks.

To address this fundamental limitation, we propose a new method, E3B, which uses an elliptical bonus at the episode level that can be seen as a natural generalization of a count-based episodic bonus to continuous state spaces, and that is paired with a self-supervised feature learning method using an inverse dynamics model. Our algorithm is simple to implement, scalable to large or infinite state spaces, and achieves state-of-the-art performance across 16 challenging tasks from the MiniHack suite, without the need for task-specific prior knowledge. It also matches existing methods on hard exploration tasks from the VizDoom environment, and significantly outperforms existing methods in reward-free exploration on the Habitat embodied AI environment, demonstrating that it scales to rich, high dimensional pixel-based observations and real-world scenarios.

Importance and Limitations of Count-Based Episodic Bonuses

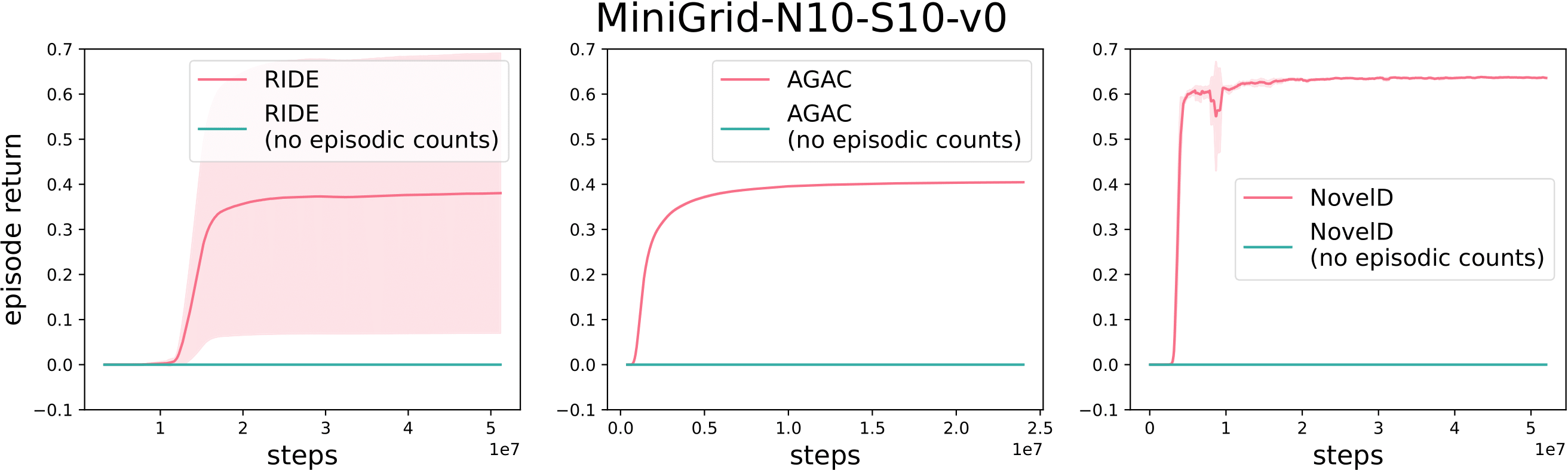
Table 1 shows the exploration bonuses used for RIDE, AGAC and NovelD - three recently proposed methods for exploration which have been applied to the MiniGrid CMDP environment. Note that all three include a term (marked in blue) which depends on episodic counts $$N_e(s)$$. Unlike count-based bonuses which are used in classical tabular RL algorithms, this count-based bonus resets after each episode. Although not presented as a central algorithmic feature, we will show below that these episodic counts are in fact essential for good performance.

Table 1. Summary of existing methods for exploring contextual MDPs. $$N_e(s)$$ denotes the number of times state $$s$$ has been observed in the current episode.

Figure 2 shows results for the three methods with and without their respective count-based episodic terms, on one of the MiniGrid environments used in prior work. When the count-based terms are removed, all three methods fail to learn. Similar trends apply for other MiniGrid environments (see our paper). This shows that the episodic bonus is in fact essential for good performance.

Figure 2: Performance of RIDE, AGAC and NovelD with and without the count-based bonus.

However, the count-based episodic bonus suffers from a fundamental limitation, which is similar to that faced by count-based approaches in general: if each state is unique, then $$N_e(s_t)$$ will always be 1 and the episodic bonus is no longer meaningful. This is the case for many real-world applications. For example, a household robot’s state as recorded by its camera might include moving trees outside the window, clocks showing the time or images on a television screen which are not relevant for its tasks, but nevertheless make each state unique. Previous works have used the MiniGrid test suite for evaluation, where observations are less noisy and do not typically contain irrelevant information. Thus, methods relying on episodic counts have been effective in these scenarios. However, in more complex environments such as MiniHack or with high-dimensional pixel-based observations, episodic count-based approaches can cease to be viable.

Elliptical Episodic Bonuses

In this section we describe Exploration via Elliptical Episodic Bonuses, (E3B), our algorithm for exploration in contextual MDPs. It is designed to address the shortcomings of count-based episodic bonuses described above, with two aims in mind. First, we would like an episodic bonus that can be used with continuous state representations, unlike the count-based bonus which requires discrete states. Second, we would like a representation learning method that only captures information about the environment that is relevant for the task at hand. The first requirement is met by using an elliptical bonus, an idea which has been previously used in the contextual bandit literature and which provides a continuous analog to the count-based bonus. The second requirement is met by using a representation learned with an inverse dynamics model.

A summary of the method is shown in Figure 3. We define an intrinsic reward based on the position of the current state’s embedding with respect to an ellipse fit on the embeddings of previous states encountered within the same episode. This bonus is then combined with the environment reward and used to update the agent’s policy.

Figure 3: Overview of E3B. State embeddings are learned using an inverse dynamics model.

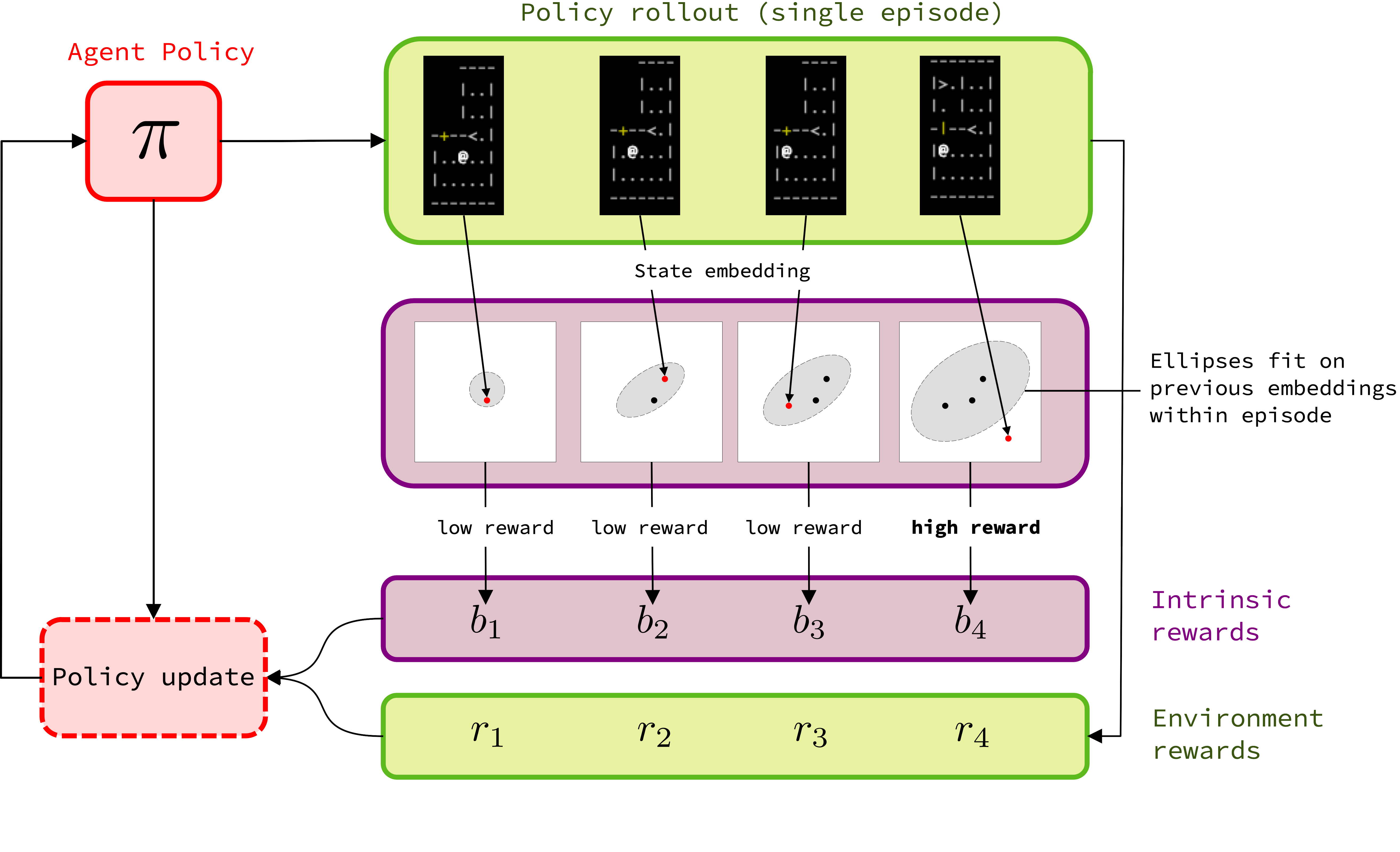
Elliptical Episodic Bonuses

Given a feature encoding $$\phi$$, at each time step $$t$$ in the episode the elliptical bonus $$b$$ is defined as follows: \begin{aligned} b(s_t) = \phi(s_t)^{\top}C^{-1}_{t-1}\phi(s_t), C_t = \sum_{i=1}^{t-1}\phi(s_i)\phi(s_i)^{\top} + \lambda I. \tag{1} \end{aligned} Here $$\lambda I$$ is a regularization term to ensure that the matrix $$C_{t-1}$$ is non-singular, where $$\lambda$$ is a scalar coefficient and $$I$$ is the identity matrix. The reward optimized by the algorithm is then defined as $$\bar{r}(s_t, a_t) = r(s_t, a_t) + \beta \cdot b(s_t)$$, where $$r(s_t, a_t)$$ is the extrinsic reward provided by the environment and $$\beta$$ is a scalar term balancing the tradeoff between exploration and exploitation.

One perspective which can provide intuition is that the elliptical bonus is a natural generalization of a count-based episodic bonus. To see this, observe that if the problem is tabular and $$\phi$$ is a one-hot encoding of the state, then $$C_{t-1}$$ will be a diagonal matrix whose entries contain the counts corresponding to each state encountered in the episode, and its inverse $$C_{t-1}^{-1}$$ will also be a diagonal matrix whose entries are inverse state visitation counts: \begin{equation*} \phi(s_i) = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \vdots \\ 0\end{bmatrix} \phantom{33} C_{t-1} = \begin{bmatrix} N_e(s_1) & & \\ \\ & \ddots & \\ & & N_e(s_n) \end{bmatrix} \phantom{333} C_{t-1}^{-1} = \begin{bmatrix} \frac{1}{N_e(s_1)} & & \\ \\ & \ddots & \\ & & \frac{1}{N_e(s_n)} \end{bmatrix} \end{equation*} The bilinear form in the bonus then reads off the entry corresponding to the current state $$s_t$$, yielding a bonus of $$1/N_e(s_t)$$: \begin{equation*} b(s_t) = \phi(s_t)^\top C_{t-1}^{-1}\phi(s_t) = \frac{1}{N_e(s_t)} \end{equation*}

For a more general geometric interpretation, if $$\phi(s_0),...,\phi(s_{t-1})$$ are roughly centered at zero, then $$C_{t-1}$$ can be viewed as their unnormalized covariance matrix. Now consider the eigendecomposition $$C_{t-1} = U^\top \Lambda U$$, where $$\Lambda$$ is the diagonal matrix whose entries are the eigenvalues $$\lambda_1, ..., \lambda_n$$ (these are real since $$C_{t-1}$$ is symmetric). Letting $$z = U\phi(s_t) = (z_1, ..., z_n)$$ be the set of coordinates of $$\phi(s_t)$$ in the eigenspace of $$C_{t-1}$$, we can rewrite the elliptical bonus as: \begin{align*} b(s_t) = z^\top \Lambda^{-1} z = \sum_{i=1}^n \frac{z_i^2}{\lambda_i} \end{align*} The bonus increases the more $$\phi(s_t)$$ is aligned with the eigenvectors corresponding to smaller eigenvalues of $$C_{t-1}$$ (directions of low data density), and decreases the more it is aligned with eigenvectors corresponding to larger eigenvalues (directions of high data density). This is illustrated below for $$n=2$$ dimensions:

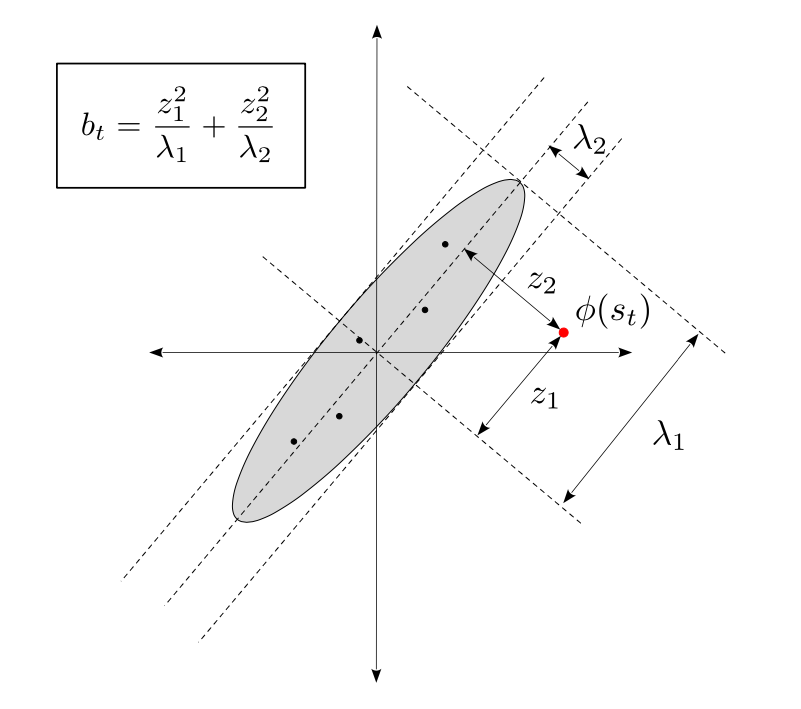
In practice, inverting the $$C_t$$ matrix at every step would be expensive, but we can use fast rank-$$1$$ updates to circumvent this - see our paper for details.

Learned Feature Encoder

Any feature learning method could in principle be used to learn $$\phi$$. Here we use the inverse dynamics model approach proposed in, which trains a model $$g$$ along with $$\phi$$ to map each pair of consecutive embeddings $$\phi(s_t), \phi(s_{t+1})$$ to a distribution over actions $$a_t$$ linking them. In our setup, $$\phi$$ is separate from the policy network. The $$g$$ model is trained jointly with $$\phi$$ using the following per-sample loss: \begin{equation*} \ell(s_t, a_t, s_{t+1}; \phi, g) = -\log p(a_t | g(\phi(s_t), \phi(s_{t+1}))) \end{equation*} The motivation is that the mapping $$\phi$$ will discard information about the environment which is not useful for predicting the agent's actions. Previous work \cite{ICM} has shown that this can make learning more robust to random noise or other parts of the state which are not controllable by the agent. In our experiments, we compare this to other approaches such as using the policy network or random networks to produce state embeddings.

Experiments

MiniHack

In order to probe the capabilities of existing methods and evaluate E3B, we seek CMDP environments which exhibit challenges associated with realistic scenarios, such as sparse rewards, noisy or irrelevant features, and large state spaces. For our first experimental testbed, we opted for the procedurally generated tasks from the MiniHack suite, which is itself based on the NetHack Learning Environment. NetHack is a notoriously challenging roguelike video game where the agent must navigate through procedurally generated dungeons to recover a magical amulet. The MiniHack tasks contain numerous challenges such as finding and using magical objects, navigating through levels while avoiding lava, and fighting monsters. Furthermore, rewards are sparse and as detailed below, the state representation contains a large amount of information, only some of which is relevant for a given task. This is illustrated below:

Note the presence of the time counter in the state - this will make each state in the episode unique, and hence will make the episodic count-based bonuses in RIDE, NovelD and AGAC meaningless. In addition to standard baselines (IMPALA, RND, ICM, RIDE, NovelD), we added three variants of NovelD which use hand-engineered features for the count-based bonus instead. NovelD-position extracts the $$(x, y)$$ position from the state and counts, NovelD-message extracts the message, and NovelD-image extracts the symbolic image. We expect these to be stronger baselelines than standard NovelD, since they remove the time counter. However, choosing which features to extract in general relies heavily on domain knowledge.

Results are shown in Figure 4. We report aggregate results across all 16 MiniHack tasks we consider, as well as results broken down by task category: what we call "navigation-based tasks", which involve things like navigating through a series of rooms (with additional challenges such as avoiding lava, opening locked doors or fighting monsters), and "skill-based tasks", which involve using objects (for example, picking up a magic wand, pointing it at a dangerous monster, zapping it, and then exiting the room).

Figure 4: Aggregate results across 16 MiniHack tasks. Bars indicate 95% confidence intervals computed using stratified bootstrapping. Methods marked with * use task-specific prior knowledge.

The standard baselines perform poorly here. For RND and ICM, this is likely due to the fact that they are designed for singleton MDPs (which are the same across episodes), and their global novelty bonus is not sufficient for contextual MDPs where the environment changes each episode. In light of our previous experiments showing that NovelD fails if the episodic bonus is removed, it is also unsurprising that standard NovelD fails here: the time counter in MiniHack makes each state in the episode unique, which has the same effect as setting the episodic bonus to a constant 1.

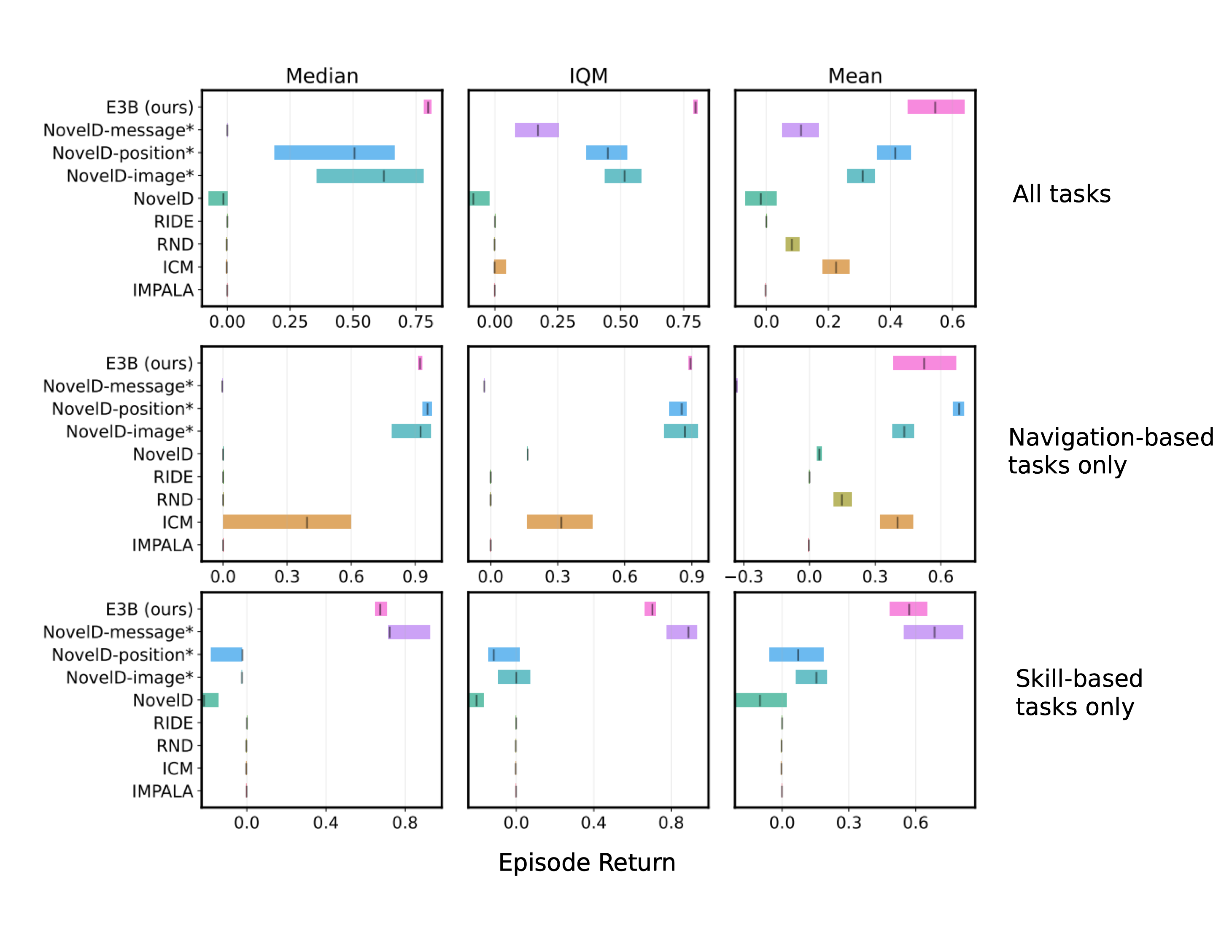
The NovelD variants which use hand-coded features for the episodic bonus perform quite a bit better. NovelD-position obtains excellent performance on navigation-based tasks, which makes sense given that constructing a count-based bonus based on $$(x, y)$$ positions will encourage the agent to visit many different $$(x, y)$$ positions over the course of the episode. However, this approach fails completely on skill-based tasks. This is because the skill-based tasks require doing things like picking up and using objects, which do not require visiting diverse spatial locations, and in this case, counting $$(x, y)$$ locations is not an appropriate inductive bias for the algorithm.

We see an opposite trend for the NovelD-message variant. This version performs very well on skill-based tasks, but much worse than the NovelD-position variant on navigation-based tasks. This highlights that when using the count-based bonus, although certain inductive biases can help for certain tasks, it is difficult to find one which performs well across all of them.

On the other hand, E3B performs well across both the navigation-based tasks and the skill-based tasks, without the need for feature engineering or prior knowledge. Out of all the methods considered, it performs the best across all three metrics

This is illustrated in Figure 5 below. The top row shows the behavior of the three methods on a navigation-based task where the agent must navigate through procedurally-generated rooms surrounded by lava to reach the goal. E3B and NovelD-position both solve the task (interestingly, NovelD-position adopts a policy which tries to maximize the number of $$(x, y)$$ locations visited in addition to reaching the goal). However, NovelD-message does not reach the goal and the agent dies by falling into the lava. This is because counting messages does not provide an intrinsic reward signal which aligns with the true reward. The second row shows the behavior of the three methods on a skill-based task, where the agent must first pick up and drink a levitation potion which will allow it to float in the air above the lava separating it from the goal. Here NovelD-position moves around but does not pick up the potion - indeed, doing does not provide it with any intrinsic reward since its intrinsic reward is constructed by counting $$(x, y)$$ locations visited. NovelD-message is able to solve the task, since picking up and drinking the potion produces novel messages of the form "f - a swirly potion", "What do you want to drink?" and "You start to float in the air!", which provide the agent with intrinsic reward.

In contrast, E3B is able to solve both the tasks, without the need for task-specific inductive biases. One explanation for its success is the following: the position information of the agent is useful for predicting movement actions, while messages are useful for predicting actions such as picking up or using objects. Therefore, it is likely that both types of information are encoded in the features extracted by the inverse dynamics model encoder.

Figure 5. Behavior of E3B, NovelD-position and NovelD-message on a navigation-based task (top) and a skill-based task (bottom).

VizDoom

As our second evaluation testbed, we used the sparse reward, pixel-based VizDoom environments used in prior work. Although these are singleton MDPs, they still constitute challenging exploration problems and probe whether our method scales to continuous high-dimensional pixel-based observations. Results comparing E3B to RIDE, ICM and IMPALA on three versions of the task are shown in Figure 6. IMPALA succeeds on the dense reward task but fails on the two sparse reward ones. E3B is able to solve both versions of the sparse reward task, similar to RIDE and ICM.

Figure 6: Results on pixel-based VizDoom. Shaded region indicates one standard deviation over 5 seeds.

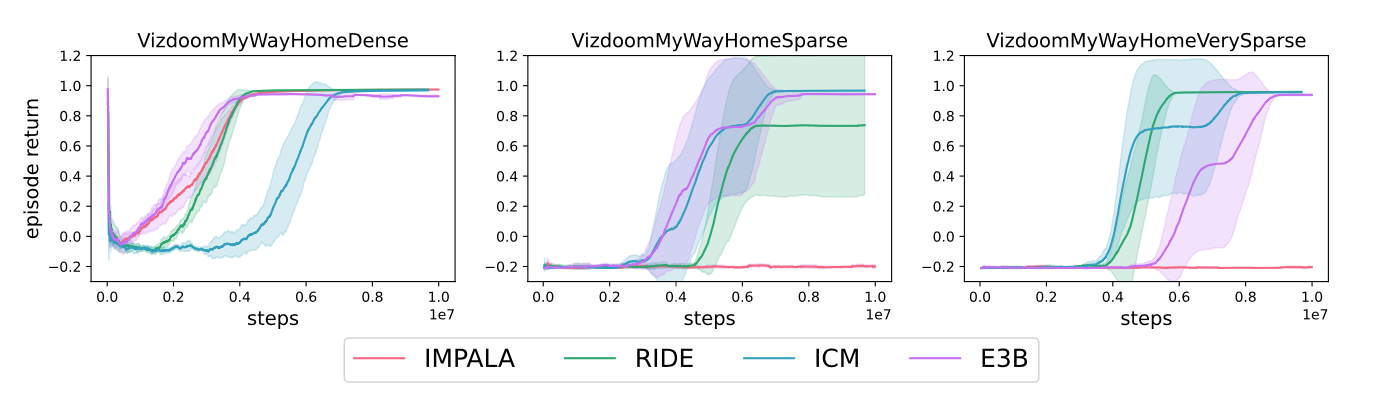
We emphasize that these are singleton MDPs, where the environment does not change from one episode to the next. Therefore, it is unsurprising that ICM, which was designed for singleton MDPs, succeeds in this task. RIDE is also able to solve the task, consistent with results from prior work. The fact that E3B also succeeds provides evidence of its robustness and its applicability to settings with pixel-based observations.

Reward-free Exploration on Habitat

As our third experimental setting, we investigate reward-free exploration in Habitat. Habitat is a platform for embodied AI research which provides an interface for agents to navigate and act in photorealistic simulations of real indoor environments. At each episode during training, the agent is initialized in a different environment, and it is tested on a set of held-out environments not used during training. These experiments are designed to evaluate exploration of realistic CMDPs with visually rich observations.

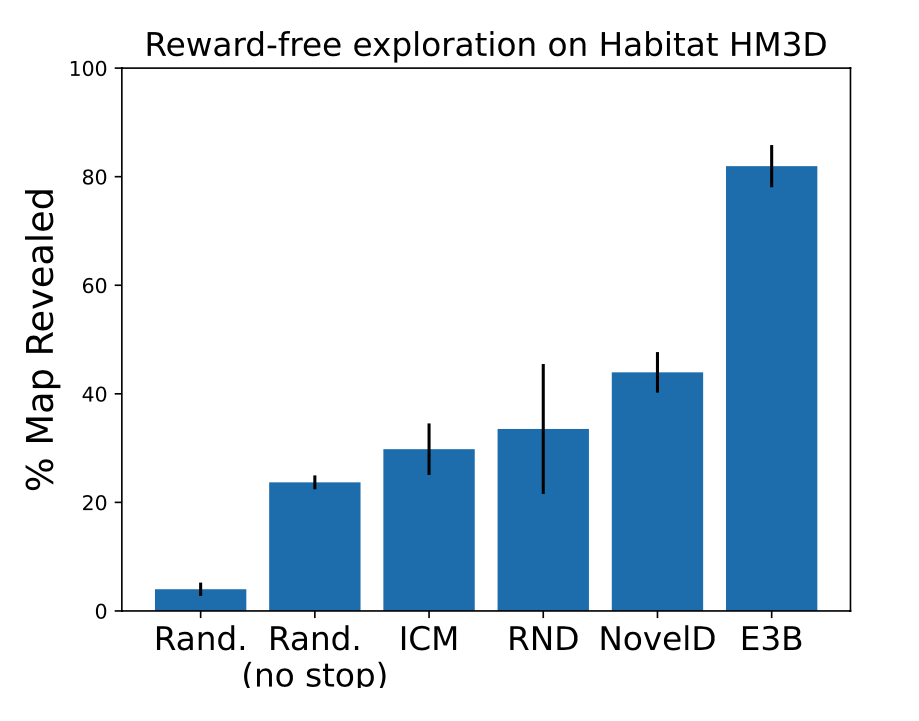
Here we train RND, ICM, NovelD and E3B agents using the intrinsic reward alone, and then evaluate each agent (as well as two random agents) on unseen test environments by measuring how much of each environment has been revealed by the agent’s line of sight over the course of the episode.

Quantitative results are shown in Figure 4, which shows that the E3B agent reveals significantly more of the test maps than any of the other agents.

Below is an example of the behavior of each of the agents. We see that the E3B agents efficiently explores most of the map, while the other agents do not. These results provide evidence for E3B’s scalability to high-dimensional pixel-based observations, and reinforce its broad applicability.

E3B NovelD RND ICM

Conclusion

In this work, we identified a fundamental limitation of existing methods for exploration in CMDPs: their performance relies heavily on an episodic count-based term, which is not meaningful when each state is unique. This is a common scenario in realistic applications, and it is difficult to alleviate through feature engineering. To remedy this limitation, we introduce a new method, E3B, which extends episodic count-based methods to continuous state spaces using an elliptical episodic bonus, as well as an inverse dynamics model to automatically extract useful features from states. E3B achieves a new state-of-the-art on a wide range of complex tasks from the MiniHack suite, without the need for feature engineering. Our approach also scales to high-dimensional pixel-based environments, demonstrated by the fact that it matches top exploration methods on Vizdoom and outperforms them in reward-free exploration on Habitat. Future research directions include experimenting with more advanced feature learning methods, and investigating ways to integrate within-episode and across-episode novelty bonuses.